How can I improve my basic knowledge about everything?

Of the close to 200 answers already posted, most claim you should expose yourself to as much of the world as you can. In truth, inundating yourself with information will only result in feeling more overwhelmed. This points to the deceptively brilliant way the OP has posed this question. And the key to seeing this brilliance is to focus on the word “basic.”

Most people, when trying to learn new things, feel pressured to quickly get through the basics; also, that memorizing these basics equates to learning. The problem is, things like basics cannot be memorized or practiced into existence. They must become a part of who you are, something that emerges in your nature; something you can never forget.

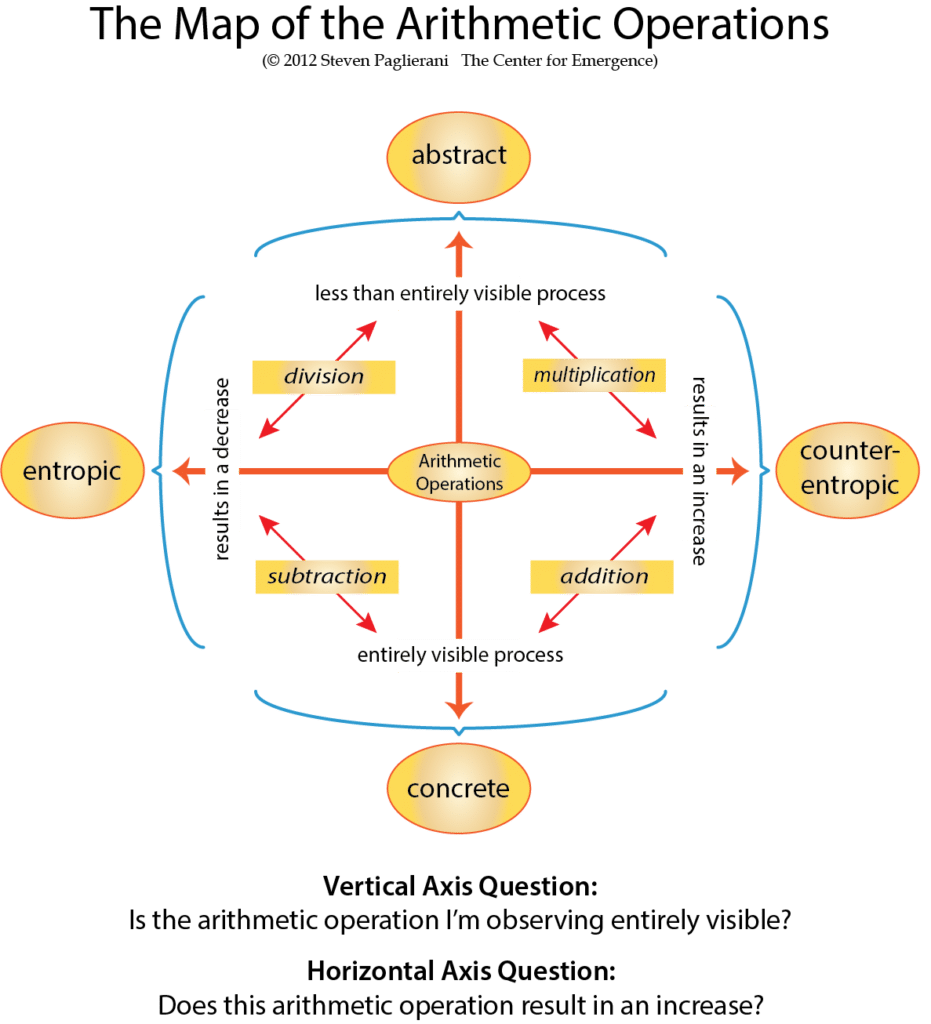
For example, take what has to be one of the most basic areas of knowledge – the four arithmetic operations: addition, subtraction, multiplication, and division. Now let me ask you. Do you think you know the basics of these four things? Most people, if asked, would quickly say, “yes.”

If this is you, then let me ask you a simple question.

What makes addition different from multiplication?

How would you answer? Do you feel certain you already know? If so, then consider this. It took me two years to discover the nature of this difference.

In the process, I discovered quite a few things I never knew, including why so many people believe they are bad at math. Meaning what? To see, I need to ask you to picture a table. On this table, there are two apples on the left side and two on the right.

Now picture what it would mean if I added these apples together. Two plus two. Obviously, it would mean that I’d slide these pairs of apples together, resulting in four apples in the center of the table.

Now at the risk of making you want to throw something at your computer screen, imagine we begin again, with two apples on the left side and two on the right. This time though, I want you to picture multiplying two apples by two apples.

Can you picture what this operation would look like on this tabletop? Certainty, you could not just slide these apples together. Sliding them together is addition, not multiplication. Strangely, picturing the outcome of adding two apples to two apples is the same as picturing the outcome of multiplying two apples by two apples. As is what you’d picture as we begin, two apples on one side and two on the other.

Are you getting the point? I’d be willing to bet that not one person reading this can tell me how this is possible. How can two obviously different arithmetic operations begin and end the same?

The answer is so obvious, once seen, that you’ll find it hard to believe no child has ever been taught this.

The beginnings and endings of both of these processes are identical. There is only one basic difference, and the drawing I’ve posted below shows it clearly. Addition, as an arithmetic operation, is entirely visible. You can picture how it starts, how things get changed during it, and how it results in the outcome. But multiplication, as an arithmetic operation, is invisible. You cannot ever picture how it changes things. You can only see how it begins and ends.

This is why children must memorize the times tables. They must memorize a matrix of outcomes, which they must them learn to generalize to larger numbers. Sadly, they never get told WHY they must memorize this table.

They must memorize this table because the operation of multiplication can never, ever be pictured.

It’s invisible.

Like I said, people spend too much time learning to ingest and regurgitate information, and not enough time learning to see the hidden-in-plain-sight basics.